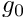In this problem we will discuss the 2D advection-diffusion problem with Neumann (flux) boundary conditions, using oomph-lib's mesh adaptation routines.
|
As always, we validate the code by choosing the boundary data and the source functions such that
![\[
u(x_1,x_2) = \tanh(1-\alpha(x_1 \tan\Phi - x_2)),
\ \ \ \ \ \ \ \ \ (4)
\]](form_11.png)
is the exact solution of the problem. The plot below shows the numerical solution for 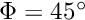
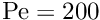
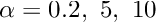
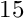
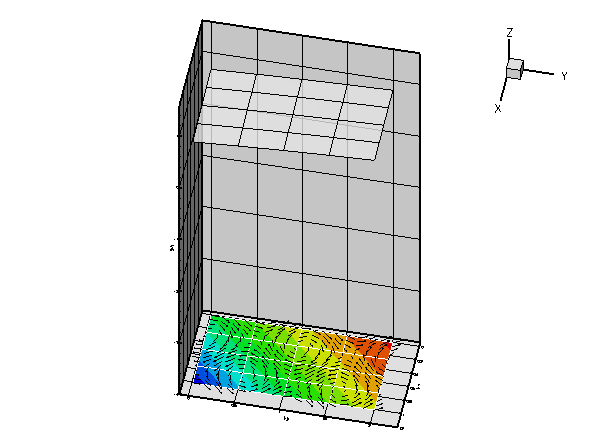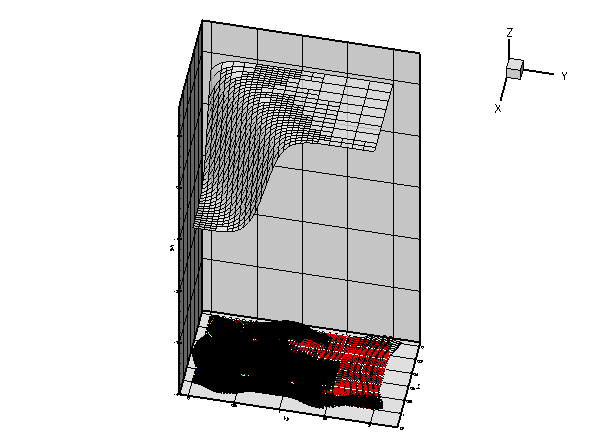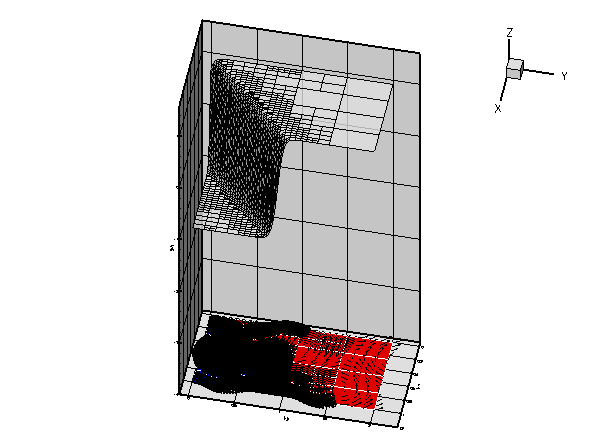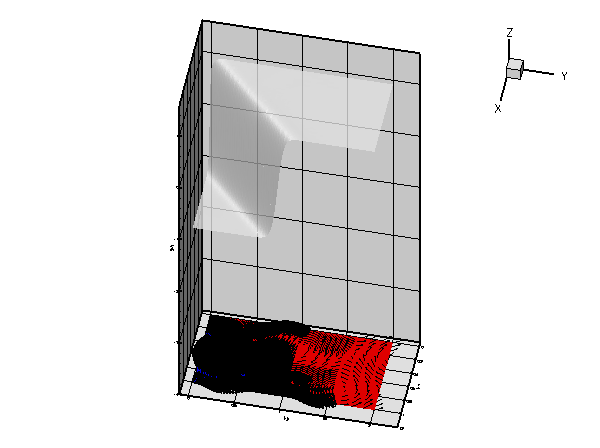
As in the example with Dirichlet boundary conditions, the unforced case is a lot more interesting. The plot below shows the result for a zero source function 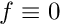

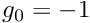
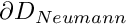
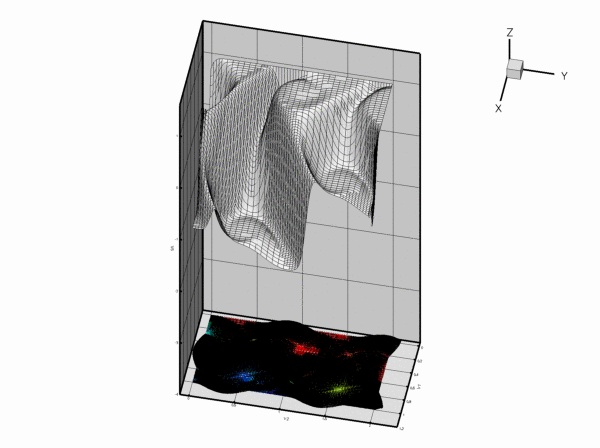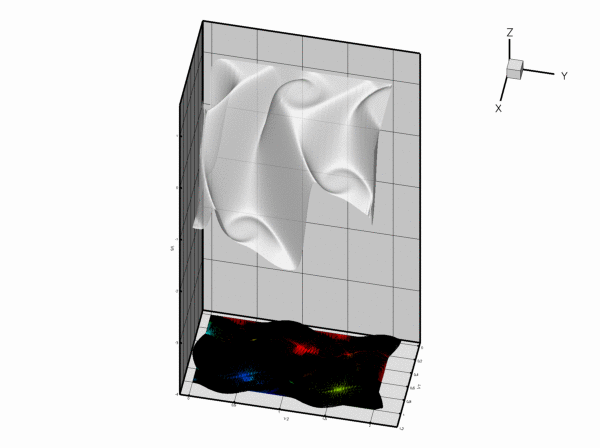
Along 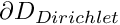
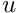
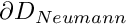
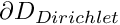
The driver code
The driver code for this problem is so similar to the corresponding Poisson problem that we do not list it here. The modifications are the same as those discussed in the advection diffusion problem with Dirichlet boundary conditions: We have to specify the wind function and the Peclet number.
Source files for this tutorial
- The source files for this tutorial are located in the directory:
demo_drivers/advection_diffusion/two_d_adv_diff_flux_bc/ - The driver code is:
demo_drivers/advection_diffusion/two_d_adv_diff_flux_bc/two_d_adv_diff_flux_bc.cc
PDF file
A pdf version of this document is available.
![\[
\mbox{Pe}\ \sum_{i=1}^2 w_i \left(x_1,x_2 \right) \frac{\partial u}{\partial
x_i} = \sum_{i=1}^2 \frac{\partial^2u}{\partial x_i^2} + f(x_1,x_2),
\ \ \ \ \ \ \ \ \ \ (1)
\]](form_0.png)
![$D =\left\{ (x_1,x_2) \in
[0,1] \times [0,2]\right\}$](form_1.png)
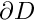
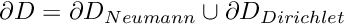
![$ \partial D_{Neumann}
= \left\{ (x_1,x_2) | x_1=1, \ x_2\in [0,2] \right\} $](form_4.png)
![\[
\left. u\right|_{\partial D_{Dirichlet}}=u_0,
\ \ \ \ \ \ \ \ \ \ (2)
\]](form_6.png)
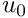
![\[
\left. \frac{\partial u}{\partial n}\right|_{\partial D_{Neumann}} =
\left. \frac{\partial u}{\partial x_1}\right|_{\partial D_{Neumann}}
=g_0,
\ \ \ \ \ \ \ \ \ \ (3)
\]](form_9.png)